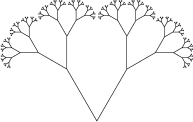
Множество заблуждений связано с фрактальностью деревьев. Древовидные объекты во многом напоминают фракталы: они строятся итеративно, они выглядят «фрактально», и иногда они даже являются фракталами. Однако, в большинстве случаев, это сходство является только внешним.
Давайте рассмотрим характерное дерево.

Можно ли найти его размерность подобия, как мы это делали в заметке про дробные размерности? Видно, что всё дерево подобно своим частям.
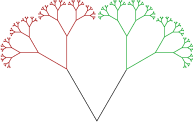
Однако не всё дерево можно составить из подобных частей. Каждая ветка действительно подобна дереву (отмечены красным и зелёным), но имеются ещё два отрезка, которые не укладываются о общую схему (чёрные). Таким образом, приведённое здесь дерево не является самоподобным объектом и искать его размерность по полученной ранее формуле нельзя.
Тем не менее, легко можно создать деревья, которые будут полностью самоподобны.
Чтобы сделать наше дерево самоподобным, нам просто надо заменить отрезки, которые нарушали самоподобие, на деревья. Например так:
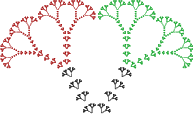
Здесь видно, что большое дерево полностью составлено из своих маленьких подобий. Два поддерева имею коэффициент подобия 0.55 (красное и зелёное), а восемь деревьев, составляющих «ветки» — 0.08 (все восемь — чёрные).
Размерность этого дерева легко вычисляется и равна примерно 1.3788.
Можно сделать ветки более тонкими. Давайте удвоим количество под-деревьев в «ветках» и вдвое уменьшим их размер:

Размерность этого фрактала 1.3455.
Если мы ещё раз удвоим количество маленьких копий дерева в «ветках» и ещё раз уполовиним размер этих копий, то получим ещё более тонкие ветки:

Размерность такого фрактала уже 1.3200.
Строго говоря, фрактал не обязательно должен быть именно самоподобен. Его фрагменты могут быть получены не только преобразованием подобия, но и любыми аффинными преобразованиями.
С помощью аффинных преобразований можно сделать «ветки» тоньше, просто деформировав, составляющие их, части дерева.

Про то, как вычисляются размерности самоаффинных объектов я напишу как-нибудь на досуге, а здесь просто скажу, что размерность этого фрактала 1.7251.
Подсчёт размерности дерева зависит от того, как вы его строите.
Например, вы можете считать, что это самоаффинный фрактал, у которого фракталы-ветки выродились в отрезки. Здесь надо понимать, что ветка, в этом случае, не является просто отрезком. В каждой точке происходит наложение бесконечного числа точек, принадлежащих разным веткам сплюснутого в отрезок фрактала. То есть при таком построении дерево не состоит из отрезков, а строится из гораздо более «тяжёлых» составляющих. Для дерева с рассматриваемыми пропорциями размерность составит 1.1594.
Но если вы строите дерево честно — из отрезков, то его размерность будет просто 1. Больше того, если сумма коэффициентов подобия меньше единицы, то можно легко вычислить протяжённость всех веток (по формуле для суммы геометрической прогрессии). То есть дерево становится не просто одномерной линией, но ещё и имеет конечную длину.
Надеюсь я пролил некоторый свет на природу «фрактальных» деревьев, вокруг который, пожалуй, больше всего недопонимания и спекуляций.