Эта статья появилась в результате любопытной переписки с utemov@*. Спасибо ему за интересные мысли и вопросы.
На первый взгляд, формула для вычисления размерности может дать мнимые корни.
Приведу пример.
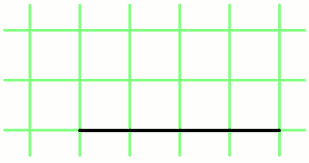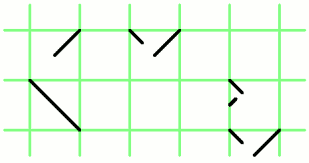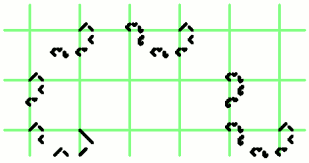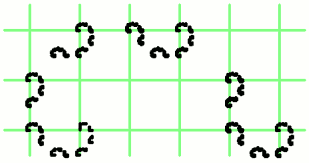
Допустим фрактал строится таким образом, что на каждом шаге итерации количество элементов удваивается и коэффициенты масштабирования для каждого элемента в новых парах таковы:
Вот как может выглядеть построение такого фрактала (разметка добавлена, чтобы было очевидно, что коэффициенты масштабирования выбраны именно указанные выше).

По полученной ранее формуле размерность получается равной:
Но к этому вопросу можно подойти и иначе.
Согласно формуле для размерности
получаем в нашем случае
Делая замену
получаем кубическое уравнение:
Решив его, можно получить D:
В нашем случае, уравнение имеет три корня (вычислены по формуле Кардано):
что соответствует трём значениям размерности:
Строго говоря, из-за логарифма, появляется слагаемое
и корней получается бесконечно много, но вернёмся к нашей тройке.
Первый (действительный) корень нам уже знаком, но появляются ещё два мнимых корня, которые удовлетворяют всем уравнениям и (казалось бы) могут претендовать на звание размерности.
Однако, давайте разберёмся, есть ли у комплексной размерности физический смысл?
Итак, вспомним, каков смысл размерности? Она связывает две другие характеристики: размер (L) и меру (M).
Размер не может быть комплексным. Это просто расстояние измеренная линейкой. Мера, традиционно, тоже является действительной. По своему физическому смыслу она родственна массе.
Однако, если размерность становится комплексной, то и мера сразу же тоже становится комплексной.
Это выглядит как-то странно, хотя это никак не противоречит определению меры. Комплексная мера полностью сохраняет свойство аддитивности, а больше от неё ничего не требуется.
Итак, комплексная размерность приводит к появлению комплексной меры. Это несколько нетрадиционно, однако, никакого криминала в этом нет.
Если вы можете допустить существование комплексной меры, то можно рассматривать комплексную размерность. Но есть и другой вопрос: даст ли это рассмотрение вам какие-либо новые знания?
Видимо, ответ на последний вопрос будет отрицательным.
В данном случае переход к комплексной размерности и мере, сродни переходу к другой системе единиц в физике. Вы можете перейти от килограммов к граммам, это приведёт к некоторому изменению формул, но не даст вам никаких новых знаний. Все рассматриваемые величины изменятся так, что зависимости между ними сохранятся. Вы не получите новых зависимостей и не получите никаких новых знаний.
Точно так же вы могли бы, например, переформулировать таблицу умножения, домножив каждый множитель на i, а произведения на -1:
... ... ... ...
... 3i * 5i = -15 3i * 6i = -18 ...
... 4i * 5i = -20 4i * 6i = -24 ...
... 5i * 5i = -25 5i * 6i = -30 ...
... 6i * 5i = -30 6i * 6i = -36 ...
... ... ... ...
Такая таблица умножения абсолютно справедлива, но ценности в ней нет никакой.